
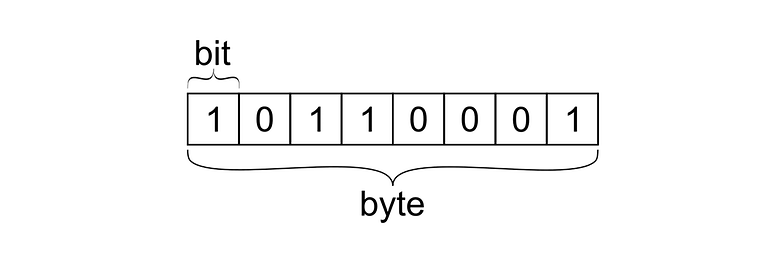
Example: Statement (1<<3) returns 8 (in Binary: 0000 1000 ), see the binary 3rd (count from 0 to 7) bit is SET here. To do this, OR the original value with a binary value of the same size with 1s in all the positions to. Here, NUM is the number whose bit you want to check and N is the bit number, (1< Finally, we get the (~pos & 31) expression. Setting individual bits uses the bitwise logical OR. Historically, the byte was the number of bits used to encode a single character of text in a computer 1 2 and for this reason it is the smallest addressable unit of memory in many computer architectures. If we do a bitwise AND ( &) operation between (31 – pos) and 31, the result remains the same. Tools The byte is a unit of digital information that most commonly consists of eight bits. Why do these two expressions have the same effects? We can deduct this process: (31 - pos) = (31 - pos) & 31Īt the beginning of this section, we mentioned the leftmost position is 31 and the rightmost position is 0, so (31 – pos) should be a positive number or zero. Just the writing of the code is subtlely different: we use (~pos & 31) to substitute the previous (31-pos) expression. We should note that the core idea has not changed. It's based on the assumption that bitwise operations are usually faster than arithmetic operations: boolean isSet = ((val << (~pos & 31)) < 0) Let's look at a rewrite of the left shift solution, which might help us achieve this. In cases where we might be performing these calculations a lot, we may wish to optimize our solution to use the least number of CPU instructions.

Set bits in a byte at specific bit positions code#


 0 kommentar(er)
0 kommentar(er)
